Quantization Fundamentals Study - 01
This is the study notes of the online course Quantization Fundamentals with Hugging Face
Table of Contents
- Data Types and Sizes - Integer
- Data Types and Sizes - Floating Point
- Example to Decode Binary String to Decimal FP32 and Vice Versa
- Downcasting
Data Types and Sizes - Integer

To check the integer ranges information in PyTorch, we can use “torch.iinfo”.
# Information of `8-bit unsigned integer`
torch.iinfo(torch.uint8)
>>> iinfo(min=0, max=255, dtype=uint8)
# Information of `8-bit (signed) integer`
torch.iinfo(torch.int8)
>>> iinfo(min=-128, max=127, dtype=int8)
# Information of `16-bit (signed) integer`
torch.iinfo(torch.int16)
>>> iinfo(min=-32768, max=32767, dtype=int16)
Data Types and Sizes - Floating Point
Three components in floating point:
- Sign (1 bit): The leftmost bit.
0for positive,1for negative. - Exponent, or range: impact the representable range of the number
- Mantissa or Fraction (precision): impact on the precision of the number
FP32, BF16, FP16, FP8 are floating point format with a specific number of bits for exponent and the fraction.
FP32
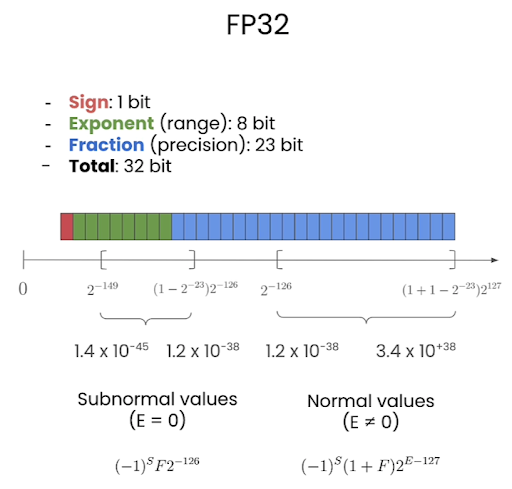
FP16
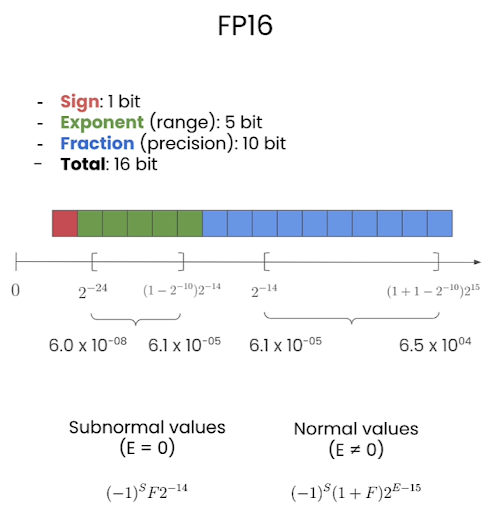
BF16
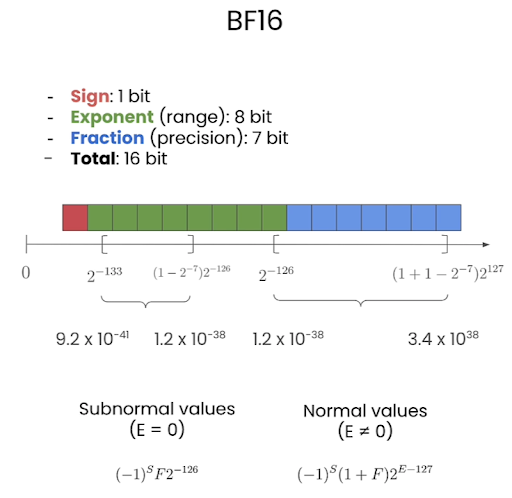
TF32 (TensorFloat-32)
TensorFloat-32 in the A100 GPU Accelerates AI Training. NVIDIA’s Ampere architecture with TF32 speeds single-precision work, maintaining accuracy and using no new code.
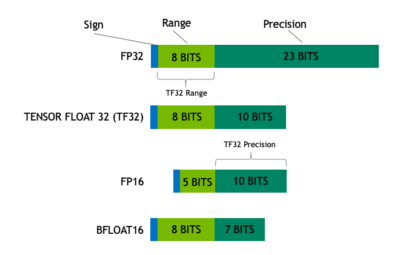
Comparison
| Data Type | Precision | maximum |
|---|---|---|
| FP32 | best | ~$10^{+38}$ |
| FP16 | better | ~$10^{04}$ |
| BF16 | good | ~$10^{38}$ 🤗 |
Floating Point in PyTorch
To check the float ranges information in PyTorch, we can use “torch.finfo”.
| Data Type | torch.dtype | torch.dtype alias |
|---|---|---|
| 16-bit floating point | torch.float16 | torch.half |
| 16-bit brain floating point | torch.bfloat16 | n/a |
| 32-bit floating point | torch.float32 | torch.float |
| 64-bit floating point | torch.float64 | torch.double |
# by default, python stores float data in fp64
value = 1/3
format(value, '.60f')
>>> 0.333333333333333314829616256247390992939472198486328125000000
# 64-bit floating point
tensor_fp64 = torch.tensor(value, dtype = torch.float64)
print(f"fp64 tensor: {format(tensor_fp64.item(), '.60f')}")
>>> fp64 tensor: 0.333333333333333314829616256247390992939472198486328125000000
tensor_fp32 = torch.tensor(value, dtype = torch.float32)
tensor_fp16 = torch.tensor(value, dtype = torch.float16)
tensor_bf16 = torch.tensor(value, dtype = torch.bfloat16)
print(f"fp64 tensor: {format(tensor_fp64.item(), '.60f')}")
print(f"fp32 tensor: {format(tensor_fp32.item(), '.60f')}")
print(f"fp16 tensor: {format(tensor_fp16.item(), '.60f')}")
print(f"bf16 tensor: {format(tensor_bf16.item(), '.60f')}")
>>> fp64 tensor: 0.333333333333333314829616256247390992939472198486328125000000
>>> fp32 tensor: 0.333333343267440795898437500000000000000000000000000000000000
>>> fp16 tensor: 0.333251953125000000000000000000000000000000000000000000000000
>>> bf16 tensor: 0.333984375000000000000000000000000000000000000000000000000000
# Information of `16-bit brain floating point`
torch.finfo(torch.bfloat16)
>>> finfo(resolution=0.01, min=-3.38953e+38, max=3.38953e+38, eps=0.0078125, smallest_normal=1.17549e-38, tiny=1.17549e-38, dtype=bfloat16)
# Information of `32-bit floating point`
torch.finfo(torch.float32)
>>> finfo(resolution=1e-06, min=-3.40282e+38, max=3.40282e+38, eps=1.19209e-07, smallest_normal=1.17549e-38, tiny=1.17549e-38, dtype=float32)
# Information of `16-bit floating point`
torch.finfo(torch.float16)
>>> finfo(resolution=0.001, min=-65504, max=65504, eps=0.000976562, smallest_normal=6.10352e-05, tiny=6.10352e-05, dtype=float16)
# Information of `64-bit floating point`
torch.finfo(torch.float64)
>>> finfo(resolution=1e-15, min=-1.79769e+308, max=1.79769e+308, eps=2.22045e-16, smallest_normal=2.22507e-308, tiny=2.22507e-308, dtype=float64)
Example to Decode Binary String to Decimal FP32 and Vice Versa
See the notebook quant_lesson01_data_types.ipynb for how to decode decimal float number to binary string, and vice versa.
From Binary String to FP32 Value
An FP32 (single-precision floating-point) number is represented according to the IEEE 754 standard and is composed of three parts:
- Sign bit: The first bit, which determines if the number is positive (0) or negative (1).
- Exponent: The next 8 bits, which represent the power of 2 by which the mantissa is multiplied.
- Mantissa (or fraction): The remaining 23 bits, which represent the significant digits of the number.
The full formula for the decimal value is:
\[(-1)^{\text{sign}}\times (1+\text{mantissa})\times 2^{(\text{exponent}-\text{bias})}\]Here is a step-by-step breakdown of how to decode an FP32 number.
1. Extract the components
Take the 32-bit binary representation of the floating-point number and divide it into its three parts.
Example: A number represented as 01000000010000000000000000000000
- Sign bit:
0(indicates a positive number) - Exponent bits:
10000000 - Mantissa bits:
10000000000000000000000
2. Decode the sign
The first bit, the sign bit, is the easiest to decode.
- If the sign bit is 0, the number is positive.
- If the sign bit is 1, the number is negative.
In the example, the sign bit is 0, so the number is positive.
3. Decode the exponent
The 8-bit exponent field is a biased representation. For FP32, the bias is 127. To get the actual exponent value, you must convert the binary exponent to decimal and then subtract the bias.
Steps:
-
Convert the exponent bits to a decimal number. In the example, the exponent bits are
10000000. \(1\times 2^{7}+0\times 2^{6}+0\times 2^{5}+0\times 2^{4}+0\times 2^{3}+0\times 2^{2}+0\times 2^{1}+0\times 2^{0}=128\) -
Subtract the bias (127) to get the true exponent, as 128-127=1
4. Decode the mantissa
The mantissa is the fractional part of the number. The IEEE 754 standard assumes a leading 1 that is not explicitly stored for normalized numbers.
Steps:
- Add the implicit leading 1 to the beginning of the mantissa bits, separated by a decimal point. In the example, the mantissa bits are
10000000000000000000000. So, the full mantissa is1.10000000000000000000000. - Convert the mantissa from binary to decimal. The places after the decimal point represent negative powers of 2.
5. Combine the parts
Now, assemble the final decimal value using the formula:
\[(-1)^{\text{sign}}\times (\text{mantissa})\times 2^{\text{exponent}}\]Applying the formula to the example:
- Sign: Positive (-1^0)
- Mantissa: 1.5
- Exponent: 1
Final calculation: \(+1\times 1.5\times 2^{1}=3.0\)
Downcasting
Advantages:
- Reduced memory footprint.
- More efficient use of GPU memory
- Enables the training of large models
- Enables larger batch sizes
- Increased compute and speed
- Computation using low precision (fp16, bf16) can be faster than fp32 since it requires less memory.
- Depends on the hardware (e.g., Google TPU, Nvidia A100)
- Computation using low precision (fp16, bf16) can be faster than fp32 since it requires less memory.
Disadvantages:
- less precise: We are using less memory, hence the compuattion is less precise.
Demo: fp32->bf16
# random pytorch tensor: float32, size=1000
tensor_fp32 = torch.rand(1000, dtype = torch.float32)
# first 5 elements of the random tensor
tensor_fp32[:5]
>>> tensor([0.3569, 0.1276, 0.5803, 0.1392, 0.2387])
# downcast the tensor to bfloat16 using the "to" method
tensor_fp32_to_bf16 = tensor_fp32.to(dtype = torch.bfloat16)
tensor_fp32_to_bf16[:5]
>>> tensor([0.3574, 0.1279, 0.5820, 0.1396, 0.2383], dtype=torch.bfloat16)
# tensor_fp32 x tensor_fp32
m_float32 = torch.dot(tensor_fp32, tensor_fp32)
>>> tensor(333.6088)
# tensor_fp32_to_bf16 x tensor_fp32_to_bf16
m_bfloat16 = torch.dot(tensor_fp32_to_bf16, tensor_fp32_to_bf16)
>>> tensor(334., dtype=torch.bfloat16)